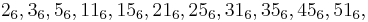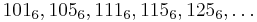Senary

Numeral systems by culture
Hindu-Arabic numerals
Western Arabic (Hindu numerals)
Eastern Arabic
Indian family
Tamil		 Burmese
Khmer
Lao
Mongolian
Thai
East Asian numerals
Chinese
Japanese
Suzhou		 Korean
Vietnamese
Counting rods
Alphabetic numerals
Abjad
Armenian
Āryabhaṭa
Cyrillic		 Ge'ez
Greek
Georgian
Hebrew
Other systems
Aegean
Attic
Babylonian
Brahmi
Egyptian
Etruscan
Inuit		 Kharosthi
Mayan
Quipu
Roman
Sumerian
Urnfield
List of numeral system topics
Positional systems by base
Decimal (10)
2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 20, 24, 30, 36, 60, 64
Non-positional system
Unary numeral system (Base 1)
List of numeral systems

In mathematics, a senary numeral system is a base-6 numeral system.

Senary may be considered useful in the study of prime numbers since all primes other than 2 and 3, when expressed in base-six, have 1 or 5 as the final digit. Writing out the prime numbers in base-six (and using the subscript 6 to denote that these are senary numbers), the first few primes are

2_6,3_6,5_6,11_6,15_6,21_6,25_6,31_6,35_6,45_6,51_6,
101_6,105_6,111_6,115_6,125_6,\ldots

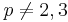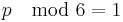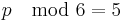That is, for every prime number p with p\ne 2,3, one has the modular arithmetic relations that either p\mod 6 = 1 or p\mod 6 = 5: the final digits is a 1 or a 5. This is proved by contradiction. For integer n:

Furthermore, all known perfect numbers besides 6 itself have 44 as the final two digits when expressed in base 6.

Contents

Finger counting

Senary multiplication table
1 2 3 4 5 10
2 4 10 12 14 20
3 10 13 20 23 30
4 12 20 24 32 40
5 14 23 32 41 50
10 20 30 40 50 100

Each regular human hand may be said to have six unambiguous positions; a fist, one finger (or thumb) extended, two, three, four and then all five extended.

If the right hand is used to represent a unit, and the left to represent the 'sixes', it becomes possible for one person to represent the values from zero to 55senary (35decimal) with their fingers, rather than the usual ten obtained in standard finger counting. e.g. if three fingers are extended on the left hand and four on the right, 34senary is represented. This is equivalent to 3 × 6 + 4 which is 22decimal.

Which hand is used for the 'sixes' and which the units is down to preference on the part of the counter, however when viewed from the counter's perspective, using the left hand as the most significant digit correlates with the written representation of the same senary number.

Other finger counting systems, such as chisanbop or finger binary, allow counting to 99 or even 1,023.

Fractions

Because six is the product of the first two prime numbers and is adjacent to the next two prime numbers, many senary fractions have simple representations:

Decimal Senary
1/2 0.5 1/2 0.3
1/3 0.3 1/3 0.2
1/4 0.25 1/4 0.13
1/5 0.2 1/5 0.1
1/6 0.16 1/10 0.1
1/7 0.142857 1/11 0.050
1/8 0.125 1/12 0.043
1/9 0.1 1/13 0.04
1/10 0.1 1/14 0.03
1/11 0.090 1/15 0.03134524210
1/12 0.083 1/20 0.03
1/13 0.0769230 1/21 0.0243405312150
1/14 0.0714285 1/22 0.023
1/15 0.06 1/23 0.02
1/16 0.0625 1/24 0.0213
1/18 0.05 1/30 0.02

(Overline represents an infinitely repeating digit, or sequence of digits.)

Natural languages

The Ndom language of Papua New Guinea is reported to have senary numerals.[1] Mer means 6, mer an thef means 6×2 = 12, nif means 36, and nif thef means 36×2 = 72. Proto-Uralic is also suspected to have used senary numerals.

See also

References

  1. ^ Owens, Kay (2001), "The Work of Glendon Lean on the Counting Systems of Papua New Guinea and Oceania", Mathematics Education Research Journal 13 (1): 47–71, doi:10.1007/BF03217098, http://www.uog.ac.pg/glec/Key/Kay/owens131.htm 

Closely related number systems

External links